プロジェクトオイラー 問９１

プロジェクトオイラーの問題をpythonでやってみます。
日本語翻訳サイトは、プロジェクトオイラー日本語 でネット検索です。

問９１「整数座標における直角三角形の個数」
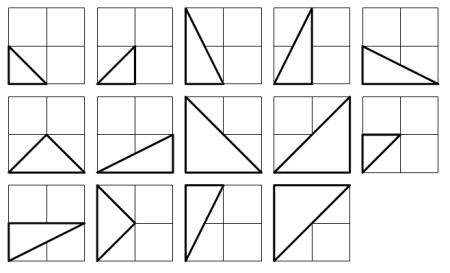
点P(x1, y1)と点Q(x2, y2)はともに整数係数の点であり, 原点O(0,0)と合わせてΔOPQをなす.

各係数が0と2の間にあるとき, すなわち0≦x1, y1, x2, y2≦2のとき, 直角三角形は14個できる:

では, 0≦x1, y1, x2, y2≦50のとき, 直角三角形は何個作れるか?





注意！！！
自力で解きたい人へ
以降の記述には解法に関するネタバレが含まれます。






私の回答例は以下の通りです。

def f(n):
	c = 0
	L = [(i, j) for i in xrange(n+1) for j in xrange(n+1)][1:]
	for x1, y1 in L:
		for x2, y2 in L:
			if x1==x2 and y1==y2: continue
			if not (x1*(x1-x2)+y1*(y1-y2)) \
			or not (x2*(x1-x2)+y2*(y1-y2)) \
			or not (x1*x2+y1*y2): c += 1
	return c//2

n = 50
print f(n)

２点P，Qの座標を総当りで作り出します。
0からnまでの数の重複を許す組み合わせをP, Qの座標候補リストLとします。
Lは内包表記に二重ループを入れてみました。
ただし、三角形なので３点O,P,Qはそれぞれ別の座標なので、まず点O(0,0)を除きます。
P(x1,y1),Q(x2,y2)のそれぞれの座標を二重ループで取得します。
まず点P,Qが同じ座標ならば三角形にならないので次の座標へ処理を進めます。

直角三角形か判定は、ベクトルの内積が0になることを利用します。
点Pが直角：ベクトルOPとベクトルQPの内積、x1*(x1-x2)+y1*(y1-y2) = 0
点Qが直角：ベクトルOQとベクトルQPの内積、x2*(x1-x2)+y2*(y1-y2) = 0
点Oが直角：ベクトルOPとベクトルOQの内積、x1*x2+y1*y2 = 0
数字の0は論理的にFalseなので、(not 内積値)で直角三角形であることを判定します。
行末の「\」は改行してもまだ同じ行と見なす継続行であることを示します。


解答はこのすぐ下の行です。文字の色を白にしてます。選択状態にすると見えます。
14234